Unveiling the Fascinating World of Polycycles and Two-Faced Maps: The Encyclopedia of Mathematics and its Applications

In the vast universe of mathematics, certain concepts stand out for their intricate beauty and wide-ranging applications. One such concept is that of polycycles and two-faced maps. These fascinating mathematical constructs have garnered significant attention from researchers and enthusiasts alike, prompting scholars to compile a comprehensive encyclopedia – The Encyclopedia of Mathematics and its Applications – dedicated to exploring these intriguing subjects. In this article, we will delve deep into the world of polycycles and two-faced maps, uncovering their significance, applications, and what makes them an integral part of the mathematical landscape.

Understanding Polycycles

Polycycles, as the name suggests, are cycles comprised of multiple vertices, connected together in a chain-like structure. In simpler terms, they can be visualized as closed loops of edges and vertices. These structures hold immense importance in a variety of mathematical fields, including graph theory, topological dynamics, and computational geometry, just to name a few.

Polycycles offer a rich ground for exploring various mathematical phenomena. They can be classified based on their properties, such as the number of vertices, edges, or their connectivity. Additionally, polycycles can pave the way for studying symmetries, transformations, and even provide insights into the spatial organization of complex networks.

Geometry of Chemical Graphs: Polycycles and Two-faced Maps (Encyclopedia of Mathematics and its Applications Book 119)

by Hans Wilhelmsson(1st Edition, Kindle Edition)

4 out of 5

Language	:	English
File size	:	13711 KB
Screen Reader	:	Supported
Print length	:	316 pages

FREE

The Dual Nature of Two-Faced Maps

Two-faced maps, also known as two-sided maps or bi-geminal maps, add another layer of fascination to the realm of polycycles. These maps possess the unique property of having two distinct faces or sides. Imagine a map of a city: on one side, you have the recognizable landmarks, roads, and buildings, while on the other side, a completely different perspective unfolds. This duality opens up a multitude of possibilities for mathematical exploration and analysis.

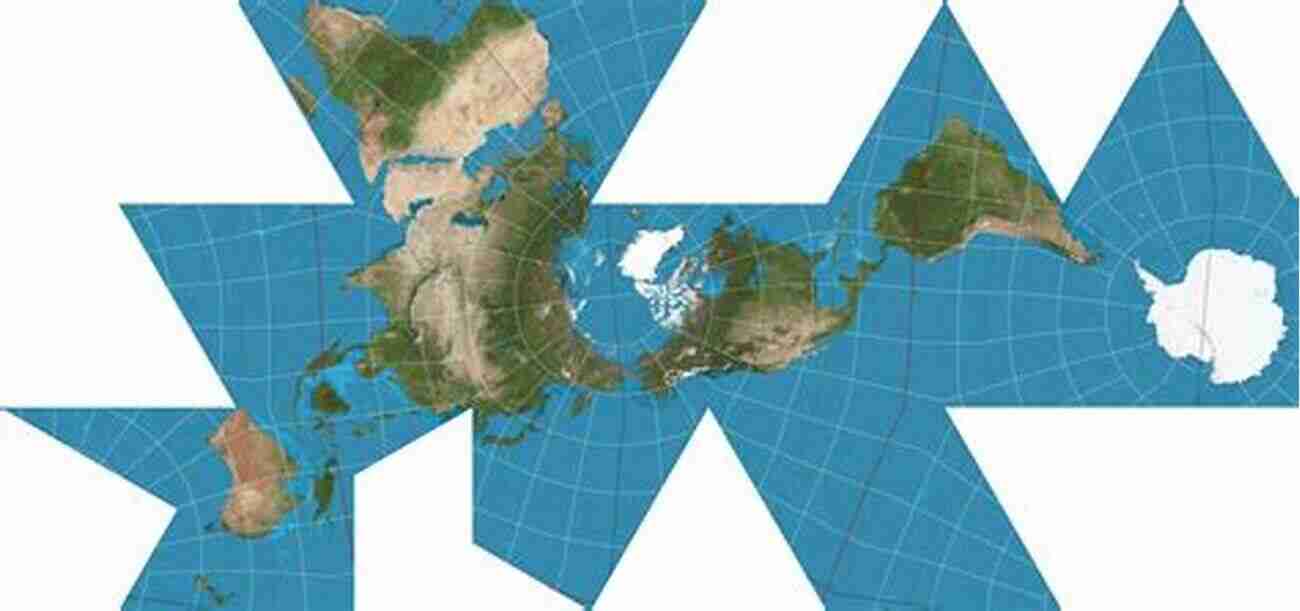
Two-faced maps find applications in diverse areas, such as combinatorics, geometry, topology, and even computer science. They provide a way to represent and study complex structures and relationships between elements. Moreover, these maps serve as a fundamental tool for understanding symmetry and duality.

The Encyclopedia of Mathematics and its Applications

To capture the richness and intricacy of polycycles and two-faced maps, The Encyclopedia of Mathematics and its Applications offers a comprehensive compendium of knowledge for mathematicians, researchers, and scholars. This iconic reference work brings together various contributions from prominent experts in the field, offering a holistic approach to understanding these concepts in all their glory.

The Encyclopedia of Mathematics and its Applications covers a vast array of topics related to polycycles and two-faced maps, from their historical origins to cutting-edge research and emerging applications. It presents a treasure trove of information, combining theoretical foundations with practical illustrations and real-world examples.

Applications in Real-World Challenges

Although polycycles and two-faced maps may seem like abstract concepts confined to the realm of mathematics, their applications extend far beyond theoretical musings. These mathematical frameworks find practical use in solving real-world challenges across a range of disciplines.

In transportation planning, the study of polycycles allows for optimizing the design and routing of roads and transportation networks. By understanding the connectivity and symmetry of polycycles, engineers can create efficient transportation systems that minimize congestion and improve overall traffic flow.

In computer science, two-faced maps provide insights into data organization and representation. They are especially relevant in designing efficient algorithms for operations such as sorting, searching, and graph traversal. The duality of two-faced maps offers an elegant way to tackle complex computational problems.

Polycycles and two-faced maps represent just a glimpse into the depths of the mathematical universe. These captivating concepts, with their intricate structures and dualities, have captivated mathematicians for centuries. The Encyclopedia of Mathematics and its Applications offers a portal into this mesmerizing world, providing an invaluable resource for anyone seeking to explore and understand the intricacies of polycycles and two-faced maps.

So next time you come across a convoluted road network or flip through a map, remember the hidden mathematical beauty lying beneath the surface. Polycycles and two-faced maps are the unsung heroes enabling us to navigate the complexities of the world.

Geometry of Chemical Graphs: Polycycles and Two-faced Maps (Encyclopedia of Mathematics and its Applications Book 119)

by Hans Wilhelmsson(1st Edition, Kindle Edition)

4 out of 5

Language	:	English
File size	:	13711 KB
Screen Reader	:	Supported
Print length	:	316 pages

FREE

Polycycles and symmetric polyhedra appear as generalisations of graphs in the modelling of molecular structures, such as the Nobel prize winning fullerenes, occurring in chemistry and crystallography. The chemistry has inspired and informed many interesting questions in mathematics and computer science, which in turn have suggested directions for synthesis of molecules. Here the authors give access to new results in the theory of polycycles and two-faced maps together with the relevant background material and mathematical tools for their study. Organised so that, after reading the introductory chapter, each chapter can be read independently from the others, the book should be accessible to researchers and students in graph theory, discrete geometry, and combinatorics, as well as to those in more applied areas such as mathematical chemistry and crystallography. Many of the results in the subject require the use of computer enumeration; the corresponding programs are available from the author's website.